|
Le
curve nurbs
|
|
|
123, 124- Curva CV nurbs e P nurbs |
|
|
Le
curve Nurbs: è
un ulteriore tipologia di curve, che si basa su algoritmi parametrici
differenti. Il processo di genesi di queste curve è l'interpolazione
dei punti definenti la curva. Definiti i vertici spaziali, l'algoritmo
calcola l'andamento della curva, punto per punto, in funzione delle
posizione relative dei vertici. Le curve nurbs si presentano in due
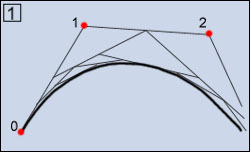
differenti forme : curve CV e curve P. Le curve CV (Control Vertex),
come quella di figura 1, sono determinate da vertici spaziali che non
giacciono sulla curva stessa. L'algoritmo calcola in pratica la curvatura
in funzione delle tangenti progressive dei CV, per tutta l'estensione
della curva. Ciò significa che modificando la posizione di un
vertice estremo, viene influenzata la curva lungo gli altri vertici.
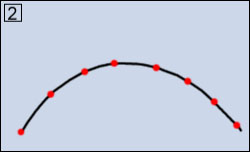
Le curve P (Point curve), mostrata in figura 2, sono definite da punti
giacenti sulla curva stessa. L'aspetto più interessante di queste
curve, è che una generica spline può essere convertita
in nurbs, l'algoritmo automatico calcola le trasformazioni relative
ai vertici non convertibili direttamente; le nurbs infatti sono curve
continue che non possono contenere punti di discontinuità, come
angoli a spigolo vivo e picchi. Da un punto di vista progettuale l'utilità
di operare attravesro le curve nurbs è dovuta alla possibilità
di costruire superfici curve estremamente complesse e senza soluzioni
di continuità. Nella mia interpretazione soggettiva dell'architettura
di Gaudì tali curve, si dimostrano efficaci nel simulare le forme
organiche delle architetture dell'autore. Le procedure generative da
me adottate si basano essenzialmente sulla costruzione di codici che
agiscono sui vertici di controllo delle curve nurbs. La difficoltà
iniziale di questo tipo di approccio è stato il passaggio obbligato
dalle ipotetiche curve di rilievo degli scenari di riferimento all'adduzione
di punti geometrici traducibili in spezzate (tramite i codici), per
ottenere in fine le curve nurbs da estrudere nelle superfici degli scenari
metaprogettuali. Non è infatti possibile determinare l'andamento
di una curva per ogni suo punto; è invece possibile determinare
una spezzata primitiva, costituita da un relativo basso numero di vertici,
su cui operare attraverso i codici generativi delle trasformazioni che
portino ad ottenere, per approssimazione, una curva nurbs corrispondente
a quella addotta inizialmente dai riferimenti. Da una spezzata si può
ottenere la corrispondente curva nurbs definita dagli stessi vertici
spaziali, il processo inverso non è invece possibile: da una
curva generica non si può risalire ai punti che l'hanno generata.
A tale proposito ho avuto una corrispondenza tramite mail, con il professore
di matematica e fondamenti di informatica Giulio Casciola dell'Università
di Bologna, Facoltà di Matematica. Chiedendogli consigli su questo
tipo di problematiche, ho avuto da lui questo chiarimento :
"Data
una curva, magari per punti, e determinare la spezzata o punti di controllo
che la definisce non e' quasi mai possibile. Le curve NURBS sono un
sottoinsieme di tutte le curve possibili, per cui assegnata una curva
non e' detto che sia una NURBS e quindi abbia una spezzata che la definisca.
Il suo problema rientra nell'approssimare la curva data (o i punti che
lei possiede) con una curva NURBS. Qui le possibilita' sono praticamente
infinite".
|