|
Appendice
sulle tecniche di modellazione utilizzate
|
|
119, 120- Curve spline con vertici morbidi
121, 122- Curve spline con vertici di Bezier |
|
Nella
costruzione delle superfici relative agli scenari di questo mio lavoro
ho utilizzato come modellatore tridimensionale 3dmax 2.5 della Kinetix
(Autodesk). Esso incorpora un modellallatore di superfici Nurbs che
si basa su particolari algoritmi parametrici di generazione di curve
continue (il termine nurbs significa : Non Uniform Rational Bicubic
Spline, cioè curve bicubiche razionali non uniformi). Tralasciando
gli aspetti puramente matematici inerenti agli algoritmi di definizione
delle curve, vediamo quali siano le particolari caratteristiche che
contraddistinguono la modellazione nurbs rispetto alla quella tradizionale
solida (tramite mesh).
Curve
spline o di Bezier : questo tipo di curve sono generate da punti
di coordinate spaziali (X,Y,Z) detti vertici. I segmenti di congiunzione
di tali vertici possono essere retti, e quindi si rientra nell'insieme
delle spezzate aperte e chiuse, comprendente ogni sorta di primitiva
2d (quadrato, triangolo, n-goni, ..ecc.); oppure i segmenti possono
essere curvi ed in questo secondo caso i vertici di controllo sono di
due tipi:
1-
vertice morbido: al vertice sono associati due punti di controllo che
giacciono sulla stessa retta. Le primitive curve come cerchi, ellissi
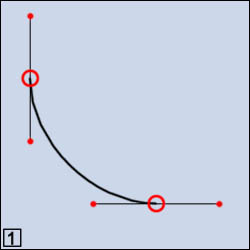
e ovoidali sono di questa categoria. In figura 1 è rappresentato
un arco di cerchio determinato da due vertici. Le relative coppie di
punti controllo giacciono sulle rispettive rette perpendicolari. In
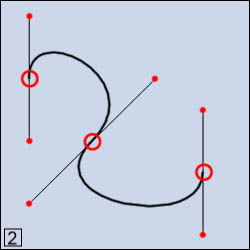
figura 2 la curva è ottenuta da 3 vertici: gli estremi sono identici
all'esempio precedente, i due punti controllo del vertice centrale giacciono
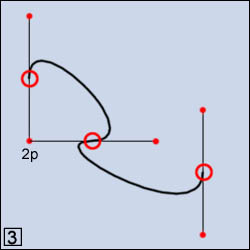
sulla stessa retta inclinata a 45°. In figura 3 gli stessi vertici
(con le stesse coordinate del piano) determinano una nuova curva in
cui la retta dei punti controllo del vertice centrale è stata
ruotata ulteriormente di 45° orari rispetto all'esempio di figura
2.
2-
vertice di Bezier : in questo caso l'algoritmo che determina la curvatura
della curva è differente; da un punto di vista geometrico, i
vertici sono determinati da due punti di controllo che però non
giacciono sulla stessa retta; sono quindi liberi di spostarsi indipendentemente
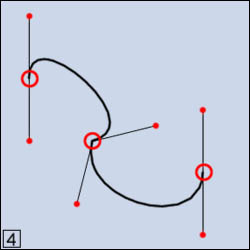
sui 3 assi (X,Y,Z). In figura 4 la curva generata possiede le stesse
coordinate di piano degli altri esempi, ma il vertice centrale è
definito da due punti controllo che non giacciono sulla stessa retta
(le rette sono ripettivamente inclinate di 30° rispetto agli assi
X e Y).
|