LA SINUOSITA'
La rotondita' delle forme e' una delle caratteristiche che maggiormente definisce la sinuosita'. In genere gli spigoli vivi
e gli angoli troppo netti non favoriscono le forme sinuose.
L'immagine della sedia riportata e' un esempio di sedia non sinuosa. Gli spigoli non presentano rotondita' e gli angoli di
raccordo tra le gambe e la seduta sono sempre perpendicolari.
|

|
CODICI DI TRASFORMAZIONE PER FORME SINUOSE
1 - LA CURVATURA DEGLI SPIGOLI
| a)
|
L'angolo di raccordo tra due o piu' spigoli o superfici potra' presentarsi vivo solo nel caso in cui sia compreso tra 150 e 210 gradi. Altrimenti dovra' presentare una curvatura il cui raggio sia compreso tra 1/4 e 1/2 della lunghezza degli spigoli che lo formano.
|

|
Il caso affrontato, quello del cubo, puo' sembrare un caso particolare, ma fa vedere in maniera chiara la trasformazione cui sono soggetti gli spoigoli del cubo.
Naturalmente le trasformazioni a cui e' soggetto non sono solo due, ma coprono tutto il campo di figure comprese tra le due mostrate.
2 - IL TAGLIO DELLE SUPERFICI
Il taglio di una superficie piana può essere eseguita in molti modi diversi, ma per renderlo sinuoso si possono seguire alcune regole:
| a)
|
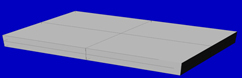
Dallo spigolo che si vuole tagliare, la linea di taglio deve partire seguendo le regole di tangenza valide per la circonferenza e continuare su questa fino a percorrerne un quarto della lunghezza. Arrivato a questo punto il taglio potrà staccarsi e seguire la linea desiderata.
|
|
| b)
|
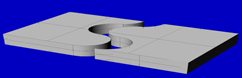
La linea di taglio dovrà formare sulla superficie una forma sinusoidale, a scelta anche non regolare, in cui la lunghezza d'onda, cioè la distanza tra le creste successive, sia al massimo uguale ad un mezzo della superficie da tagliare.
|
|
| c)
|
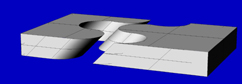
L'angolo di incidenza del taglio sulla superficie può assumere qualsiasi valore compreso tra 10 e 170 gradi.
|
|
| d)
|
Nel caso in cui le due superfici venutesi a creare vengano allontanate l'una dall'altra, se la distanza che le separa è maggiore o uguale al segmento di base di una delle due superfici, si opererà seguendo il codice sulla curvatura degli spigoli. In caso contrario lo spigolo dovrà rimanere inalterato.
|

|
|
3a - LA PIEGATURA DEGLI SPIGOLI
Codici per la piegatura di spigoli:
SPIGOLI DRITTI
| a)
|
E' possibile piegare spigoli dritti solo mantenendo costante l'angolo di curvatura. In questo modo infatti lo spigolo, da dritto, diventa un arco di circonfarenza.
|
  
|
| b)
|
Il numero di pigature effettuabili su di uno stesso spigolo è illimitato, con la sola restrizione riguardante il raggio della circonferenza su cui si appoggia la piegatura: esso infatti dovrà essere al massimo lungo la metà dello spigolo dritto.
|
|
SPIGOLI CURVI
| a)
|
Gli spigoli che già presentano una curvatura possono essere piegati liberamente come gli spigoli dritti, a condizione che il raggio della curvatura già esistente sia minore della corda che sottende l'arco formato dallo spigolo curvo.
|
|
|
|
3b - LA PIEGATURA DELLE SUPERFICI
Per effettuare una trasformazione su di una superficie dovremo modificarne gli spigoli che lo delimitano; oltre però ad utilizzare i codici illustrati in precedenza abbiamo a nostra disposizione altre alternative.
Codici per la piegatura di superfici:
| a)
|
Una delle trasformazioni applicabili ad una superficie e' l'allungamento per trazione. Per effettuare questa trasformazione si dovranno allontanare due superfici parallele ed opposte di uno stesso solido. Gli spigoli che si allungheranno, cioè quelli che si trovano tra le due superfici, non rimarranno dritti, ma presenteranno, a partire dal punto mediano, una tendenza ad avvicinarsi all'asse del solido tridimensionale. Questi spigoli diverranno perciò degli archi di circonferenza concavi verso l'interno del solido.
|
|
| b)
|
Un'altra delle trasformazioni applicabili ad una superficie e' il piegamento per torsione. Questa si verrà a creare nel momento in cui ruoterò in senso opposto due superfici parallele ma opposte di uno stesso solido. Gli spigoli si curveranno presentando una specie di esse. Il movimento di rotazione massimo che potremo dare ad una superficie sarà di 90°, in modo da non deformare in maniera eccessiva il solido.
|
|
| c)
|
Un'altra delle trasformazioni applicabili ad una superficie e' il piegamento per taglio. Questa si verrà a creare nel momento in cui sposterò una superficie parallelamente ad essa, mantenendo ferma quella parallela ma opposta. In questo caso gli spigoli che uniscono le due supefici si allungheranno e si inclineranno rispetto alla normale. L'angolo che si verrà a creare tra la normale e il nuovo spigolo non potrà essere superiore a 60°, sempre per non deformare troppo il solido.
|
|
| d)
|
Un'altra delle trasformazioni applicabili ad una superficie e' il piegamento per compressione. Questa trasformazione non è altro che quella opposta rispetto alla trazione, per cui le superfici parallele ed opposte di un solido, invece di allontanarsi, si avvicineranno. Questo fa si che gli spigoli che uniscono le due superfici si pieghino, sempre a partire dal punto mediano, formando degli archi di circonferenza convessi rispetto all'asse centrale del solido.
|
|
|
|
3c - LA PIEGATURA DEI VOLUMI
|
Anche per quanto riguarda i solidi le trasformazioni dipendono dai codici riguardanti gli spigoli e le superfici.
|
|
Questi tre insiemi di codici (3a, 3b, 3c) vanno considerati naturalmente gli uni strettamente dipendenti agli altri, infatti modificando la forma di uno spigolo di una figura tridimensionale madificheremo sia le superfici laterali di cui è composto sia il volume occupato da questo nello spazio.
|
Inizio
- Obiettivi
- Codici
- Paradigma
- Scenari
- LAB 2002
- www.artegens.com













